テキスト
流体
- 非圧縮性流体
密度が一定(縮まない)な流体 - 定常流
速度ベクトルが時間変化しない流れ - 非定常流
速度ベクトルが時間変化する流れ
動粘度(ν)=粘度(μ)/密度(ρ)
ν(ニュー)、μ(ミュー)、ρ(ロー)
ν(ニュー)、μ(ミュー)、ρ(ロー)
連続の式
- 連続の式
流れの方向に内径が変化する円管において、各断面を単位時間に通る流体の質量は一定
単位時間の質量流量(密度×断面積×平均流速)=一定
層流、乱流
- 層流
流体の各粒子がすべて流れの方向にのみ動く流れ
流速分布は放物線状
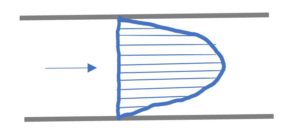
管壁に接する部分の流速は0、管中心部で最大流速
平均流速は最大流速の1/2 - 乱流
流体の各粒子が流れの方向以外にも速度を持つ流れ(渦など)
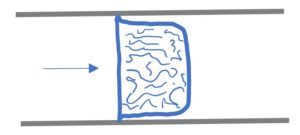
流速分布はほぼ均一
平均流速は中心流速の0.8倍 - 層流から流速を上げていくと乱流へ遷移(せんい)する
レイノルズ数
- レイノルズ数
流体の粘性力に対する慣性力の比を表す無次元数
レイノルズ数(Re)= ρ × u × d /μ
ρ(ロー):密度 u:流速
d:管の内径 μ(ミュー):粘度
ρ(ロー):密度 u:流速
d:管の内径 μ(ミュー):粘度
また、動粘度(ν)=粘度(μ)/密度(ρ)のため
レイノルズ数(Re)=u×d/ν
とも表せる
- レイノルズ数は、管の内径、平均流速、密度に比例し、粘度、動粘度に反比例する
- 臨界レイノルズ数
乱流から層流へ遷移するときの値(約2300)
ベルヌーイの式
- ベルヌーイの式
流体に関するエネルギー保存則
非圧縮性、非粘性流体の定常流で成立する
ベルヌーイの式によれば運動エネルギー、位置エネルギー、圧力エネルギーの3つの和は保存される
ρ×u2/2+ρ×g×z+p=一定
ρ(ロー):密度 u:流速
g:重力加速度 z:高さ P:圧力
※ ρ×u2/2+ρ×g×z+p=一定
運動エネルギー
位置エネルギー
圧力エネルギー
ρ(ロー):密度 u:流速
g:重力加速度 z:高さ P:圧力
※ ρ×u2/2+ρ×g×z+p=一定
運動エネルギー
位置エネルギー
圧力エネルギー
圧力損失
- 層流の圧力損失
平均流速・管の長さに比例
管内径の2乗に反比例
ハーゲンポアズイユの式で表す
- 乱流の圧力損失
平均流速の2乗・管の長さに比例
管内径に反比例
ダルシー・ワイスバッハの式で表す
動画コンテンツ
ミニテスト
第1問
第2問
第3問
過去問題
第1問
流体に関する次の記述のうち、誤っているものはどれか
第2問
直円管内の完全に発達した流れに関する次の記述のうち、誤っているものはどれか
第3問
直円管内の完全に発達した流れに関する次の記述のうち、誤っているものはどれか
第4問
流動に関する次の記述のうち、誤っているものはどれか
テキスト(計算問題)
連続の式
質量流量(Qm)=ρ×(π×d2/4)×u=一定
ρ(ロー):密度 d:管径
u:平均流速 π(パイ):円周率
※ π×d2/4→ 円の面積
{(d/2)× (d/2) ×π→半径×半径×円周率}
密度(ρ)が一定の場合、体積流量Qvは
体積流量(Qv)=(π×d2/4)
レイノルズ数(Re)
レイノルズ数(Re)= ρ × u × d /μ
ρ(ロー):密度 u:流速
d:管の内径 μ(ミュー):粘度
ρ(ロー):密度 u:流速
d:管の内径 μ(ミュー):粘度
過去問題(計算問題)
第1問

第2問

第3問





